統計誤用の問題を解決するための「統計の手引き」

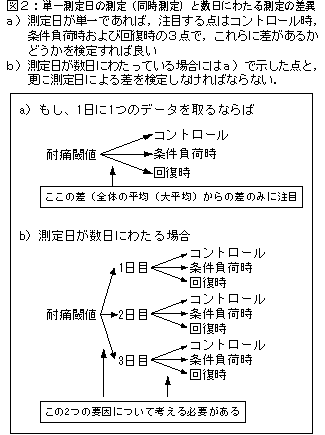
本稿は、研究計画が十分に検討されないまま実施された仮想的な研究を例題として取り上げ、その問題点を指摘していく形をとっています。十分な研究計画がなされないままに結果だけを見て統計解析を行うと、文中で指摘されているような問題が起こることをご理解いただく目的で作成しました。

全日本鍼灸学会研究部
「統計の手引き」
ワーキンググループ

高橋 則人　七堂 利幸　篠原 鼎
鍋田 智之　北小路博司　川喜田健司

はじめに

鍼灸関連の雑誌で発表されている論文の統計誤用が共著者のひとりである七堂氏によって指摘されて以来、統計誤用に関する関心は高まり、鍼灸医学に関係の深い問題を集めた「統計の手引き」を作る必要性が唱えられてきました。

学会の研究部は、旧学術部研究委員会当時からその作成に向けていろいろと協議を重ねてきましたが、その議論の当初から、いわゆるマニュアルの形で作るとそのまま鵜呑みにされて、かえって本当の意味での問題解決にならないということが指摘されていました。

そこで、適当な例題を出して、そこで生じうる問題をピックアップするということが大筋としては決まったのですが、何を具体的な例題として取り上げるのか、いろいろと議論を重ねてきているところです。

この間、統計誤用の問題に関する問題は、鍼灸学会ばかりではなく、広く医学会や心理学の分野で注目を集め、活発な議論が行われるようになっています。

そこで、完成した形とは言いかねますが、討論の材料として、これまでの議論の一部を紹介することにしましたので、参考にしていただきたいと思います。

本稿は、研究計画が十分に検討されないまま実施された仮想的な研究を例題として取り上げ、その問題点を指摘していく形をとっています。十分な研究計画がなされないままに結果だけを見て統計解析を行うと、文中で指摘されているような問題が起こることをご理解いただきたいと思います。

今回の例題では、全日本鍼灸学会誌でも頻繁に見られる統計学的な問題として、同時比較（同時測定）でない研究、多重性の問題、タイプ１エラーおよびｔ検定の誤用（多期比較、いわゆる輪切り検定）について取り上げました。また用語解説を載せてありますので参考にして下さい。

例題Ⅰ経穴Ａへの鍼刺激が
経穴Ｂの耐痛閾値に及ぼす影響。

方法

ある経穴（経穴A）への鍼刺激が別のある経穴（経穴B）の耐痛閾値に与える影響を、コントロール時、条件負荷時および回復期の３つの時点で、プッシュプルゲージを用いて測定を行った。測は、最初にコントロール時の経穴Bの閾値を測定し、10分後に経穴Aに鍼刺激を10分間行い、刺激終了直後に経穴Bの閾値（条件負荷時）を測定し、さらにその10分後に経穴Bの閾値（回復期）を測定した。

この研究に5人の被検者が参加した。被検者Aは1日1回、3日連続で測定を行い、被検者Bは1日1回、1日間隔で5日間、すなわち3つのデータセットを得、被検者Cは1日3つのデータセットを得た。被検者Dは1回のみ測定し1つのデータセットを得た。被検者Eは1日に1つのデータセットを得、1週間後にさらにもう1つのデータセットを得た（表１）

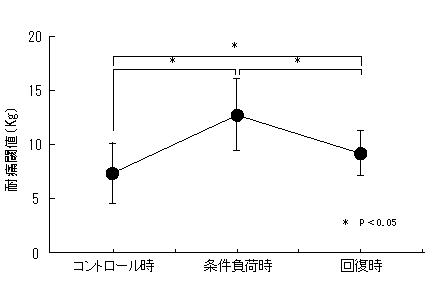
図１：耐痛閾値の経時的変化

グラフ縦軸は耐痛閾値，横軸は各測定時期を示す．値は平均と標準偏差を示す．耐痛閾値は鍼刺激を与えると有意（p<0.05）に上昇し，回復時においてもコントロール時と比較して有意（p<0.05）に増加していた。

なお統計はｔ検定を用い、解析ソフトにはMacintosh 版 STATISTICA 4.1J を用いた。

結果

等分散性の検定（バートレット検定）と記述統計を表２、３に、生データを表４に、結果をグラフ化したものを図１に示す。ｔ検定の結果、コントロール時と条件負荷時ではｔ値が－7.00543でｐ値が0.0000225、条件負荷時と回復時ではｔ値が4.912670でｐ値が0.0004622.コントロール時と回復時ではｔ値が－2.28448でｐ値が0.0431950であった（図中の星印はｐ＜0.05）。

考察

以上の結果から、経穴Aへの鍼刺激は、経穴Bの耐痛閾値を増加させ、その効果は鍼刺激10分後でも持続している事が示唆された。（注意：この例題に提示した数値データは仮想データです）

全般的な問題点

この研究の最大の問題点は、事前の研究計画が綿密になされていないことです。まず研究の目的を明確にする必要があります。この例題では「ある経穴（経穴A）への鍼刺激による経穴Ｂの耐痛閾値への影響を調べる～」となっていますが、研究者の真の目的は何でしょうか？つまり、「コントロール時（刺激前）に比較して後の２時期の耐痛閾値に差があるかどうか」ということになると思われます。そうなると２群間の比較を繰り返すこと（ｔ検定を用いること）は適切ではありません。多重比較を用いなくてはなりません。

また検定法は研究計画を立てるプロセスの中で、サンプルサイズ（対象の数）を決定する際におのずと決まってくるもので、「このような研究結果（測定データ）に対してどのような統計法を用いるか？」というプロセスは、本来あり得ないはずなのです。臨床研究で用いられている検定法は、実際のデータを取得する前に決定しておくべきであり、そのためには十分に研究計画を練らなければなりません。そうすることによって、現在のいわゆる「統計の問題」というのは存在しなくなるはずです。そればかりか、その臨床研究の価値を向上させることにもなるのです。

ではこの例題にあるような臨床研究の問題点をあげ、予想される批判とその根拠を列挙してみましょう。

同時比較でない

まず同時比較でないことがあげられます。この研究の中で強いて同時比較として見ることが出来るのは測定日１の①,④,⑦,⑩,⑪の５つのデータセットだけです。つまり５人の被検者から５つのデータということになります。同時期に比較しないと、気候変動などの比較時の条件が異なっていたりした場合に、結果に大きく影響を与える可能性があります。特に被検者Cは１日に３回もの測定を行っており（同時比較性を言いかえれば）、もし測定値が測定日と交互作用があれば、測定値は独立とはいえず、測定日にも影響されていることになります。

表1：被験者と測定日およびサンプリング
被験者と測定日およびサンプリングを行った時期を表にして示した。この表からも分るように、実際には5名しか参加していない研究から12個のデータを得ている。

測定日	1	2	3	4	5	6	7	8
被験者A	①	②	③
被験者B	④		⑤		⑥
被験者C	⑦⑧⑨
被験者D	⑩
被験者E	⑪							⑫

表2：等分散性検定（バートレット検定）
今回得られたデータが、各時期において正規分布をしているかどうかを検定した結果。
水準Pが0.05以上なので、得られたデータは正規分布している（各測定時期間で測定値の分布に明らかな偏りがない）ことを示している。多重比較する場合にも、この等分散検定を事前に行う必要がある。

ハートレイF-最大	コクランC	バートレットｘ2乗	自由度	水準P
0.5934261	0.1113395	2.282912	2	0.3193667

表3：記述統計結果
今回得られたデータの記述統計をまとめた表。用いる統計ソフトにより若干計算される項目名が異なる。

二つの要因がお互いに影響しあう効果を交互作用と言います。この例題では、要因１が測定日（１日目、２日目など）で、要因２が各々の時期（コントロール時、条件負荷時および回復時）に測定された耐痛閾値となります。ちなみに一つの要因の単独効果を主効果といいます。図２で説明すると、もし１日に一つのデータを取るのであれば、耐痛閾値がコントロール時、条件負荷時および回復時の３つの期間でどれだけ全体の平均値から差があるかを検討するだけで済みますが、測定が何日かにわたると、加えて測定日による差についても考えなければいけません。すなわち要因１（測定日）による差、要因２（時期）による差の他に、要因１と要因２がお互いに影響して生じた差（交互作用による差）および偶然による差の４つについて注目しなければなりません。同時対照比較ではないこの例題の研究目的を上記のように考えると、「測定日によって耐痛閾値が変化するのか？時期によって変化するのか？あるいは測定日と時期が複雑に絡みあって耐痛閾値に影響を及ぼすのか？」という解釈になってしまい、当初の目的と食い違ってきます。

タイプ１のエラー：第一種の過誤、type 1 error

実際には帰無仮説が真であるにもかかわらず、結果が統計学的に有意と考え、帰無仮説を棄却してしまう過誤を指します。例題では、耐痛閾値が鍼刺激によって全く変化しないのが事実（帰無仮説が真）だとすると、適切な統計処理を行えば有意差が出なかったかもしれないところを、ｔ検定の誤用により、計算上ではｐ値が0.05以下となってしまい、研究者はこの計算結果を信じ、帰無仮説を棄却して、対立仮説を採用し、耐痛閾値は鍼刺激によって変化すると結論を出してしまうことです。これをタイプ１エラーといいます。αで表され、通常（習慣上）0.05に設定されます。
またタイプ２エラー（第二種の過誤：type 2 error）というのも存在します。これは実際には帰無仮説が偽であるにも関わらず、結果が統計学的に有意でないと考え、帰無仮説を採用してしまう過誤を指します。βで表され（１－β）を検出力と呼び、サンプルサイズの設計に使います。これは研究計画の中でサンプルサイズを十分に検討していれば避ける事が出来る過誤です。この２つの関係を図3に示します。

図3：事象の心理と研究による結果との関係
事象の真理を知るには、全てのサンプル（対象が日本人男性であればその全て）を対象とすることが望ましいが、現実には不可能である。そこで我々は母集団（例えば日本人成人男性の一部）から（無作為に）サンプルを抽出し、そのサンプルから得られた結果から母集団での事象を推定する。その推定が正しく導かれていればポジティブな結果であれネガティブな結果であれ、研究結果とは結論は正しく母集団を推定できていることになる。母集団の真理と研究結果の食い違いにはタイプ１エラーとタイプ２エラーがある。いずれも母集団の真理は不変であるので、過誤は研究結果の方にある。

	母集団における真理（研究目的としている事象の真実） 鍼刺激により耐痛閾値が変化するかどうか？
サンプル集団における研究結果 （研究で得られたデータ）		鍼刺激により耐痛閾値が変化するのが真実	鍼刺激により耐痛閾値が変化しないのが真実
	帰無仮説を否定 （変化すると結論）	正しい研究結果と結論 （鍼刺激により耐痛閾値は変化する）ポジティブな結果	タイプ１エラー
帰無仮説を採用（変化しないと結論）		タイプ２エラー	正しい研究結果と結論（鍼刺激により耐痛閾値は変化しない）ネガティブな結果

図4：多期検定によるタイプ1エラーの増加
多期検定によるタイプ1エラーの増加は、サイコロによる確率の計算で考えてみるとわかりやすい。同じ事を繰り返す（サイコロを何回も振ったり、ｔ検定を何回も行う）事により我々は知らず知らずのうちにタイプ1エラーを増加させてしまう。

繰り返し検定の問題

なぜ多期にわたってｔ検定を用いてはいけないのでしょうか？なぜコントロール群と条件負荷時（以下C対S）、コントロール時と回復時（以下C対R）および条件負荷時と回復時（以下S対R）とｔ検定を3回繰り返して行うのはいけないのでしょうか？
例えば「サイコロを2回振って少なくとも一回は1の出る確率」は図4に示した式より導かれます。この式を使って計算すると前述の確率は約31％と計算することが出来ます。同じように「サイコロを3回振って少なくとも一回は1の出る確率」を計算してみると、その確率は約42％になります。このように同じ事を繰り返す（サイコロを何回も振る）と、全体として1の出る確率はだんだん高くなっていきます。
ではｔ検定を3回繰り返すことは、前述の統計の基本から考えるとどの様になるでしょうか。C対S、C対RおよびS対Rの3つの組み合わせで検定を行った場合、「少なくとも1つの組み合わせに有意差が出る確率」はどの様になるでしょうか？ここで帰無仮説上「有意差がある」となる確率、いわゆる危険率は5％ですから、「有意差がない」となる確率は95％、すなわち0.95になります。そうすると全部で3回の検定を行うのですから、図4に示したような式が成り立ちます。これを計算すると約0.143となります。つまり「少なくとも一つの組み合わせに有意差が出る確率」は約14％で、我々が期待している5％よりもはるかに高い確率になってしまいます。これが4つ5つと多期検定の数が増えればどの様な結果になるかはもうおわかりになると思います。

おわりに

我が国の鍼灸関連雑誌における統計の誤用が指摘されて依頼、論文作成時に統計の問題はかなり意識されるようになってきています。そして単純な統計上の誤りは少なくなってきたように見受けられます。本稿を手始めとして、統計にまつわる様々な問題を紹介していきたいと考えていますので参考にしていただければ幸いです。また、本稿の内容について忌憚のないご意見をお聞かせ下さい。
心理学の立場から統計誤用の問題にご意見をいただき、また単一被験体法の鍼灸研究への導入に関して示唆に富む提案をいただいた、今は亡き故 桑田繁先生に心よりお礼申し上げるとともにご冥福をお祈りいたします。

参考文献（ホームページを含む）

１）向後千春：統計学がわかる: ハンバーガーショップでむりなく学ぶ、やさしく楽しい統計学（技術評論社）

２）長谷川芳典：心理研究法再考(1)基礎的統計解析の誤用をなくすための30のチェック項目
http://ousar.lib.okayama-u.ac.jp/files/public/5/53811/20160528122903888008/jfl_021_047_059.pdf

３）Hully SB and Cummings SR,木原正博監訳：医学的研究のデザイン：研究の質を高める疫学的アプローチ：メディカル・サイエンス・インターナショナル
https://ci.nii.ac.jp/ncid/BA66897160